搜题，刷题，出题，就用题百科
登录
找答案
首页>初中数学>二次函数的定义考试题目
【简答题】
手机使用
编辑在平面直角坐标系中， O是坐标原点，直角梯形 AOCD的顶点 A的坐标为 （0，
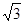），点 D的坐标为（1，
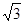），点 C在
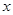轴的正半轴上，过点 O且以点 D为顶点的抛物线经过点 C，点 P为 CD的中点．
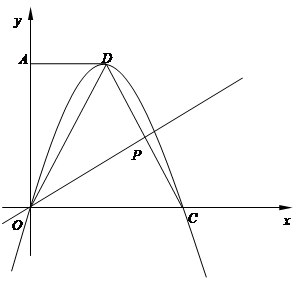（1）求抛物线的解析式及点 P的坐标； （2） 在
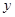轴右侧的抛物线上是否存在点 Q，使以 Q为圆心的圆同时与
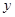轴、直线 OP相切．若存在，请求出满足条件的点 Q的坐标；若不存在，请说明理由； （3）点 M为线段 OP上一动点（不与 O点重合），过点 O、 M、 D的圆与
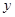轴的正半轴交于点 N．求证： OM+ ON为定值． （4）在
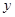轴上找一点H，使∠PHD最大．试求出点H的坐标．
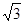），点 D的坐标为（1，
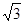），点 C在
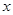轴的正半轴上，过点 O且以点 D为顶点的抛物线经过点 C，点 P为 CD的中点．
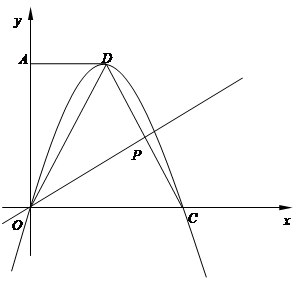（1）求抛物线的解析式及点 P的坐标； （2） 在
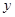轴右侧的抛物线上是否存在点 Q，使以 Q为圆心的圆同时与
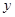轴、直线 OP相切．若存在，请求出满足条件的点 Q的坐标；若不存在，请说明理由； （3）点 M为线段 OP上一动点（不与 O点重合），过点 O、 M、 D的圆与
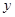轴的正半轴交于点 N．求证： OM+ ON为定值． （4）在
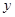轴上找一点H，使∠PHD最大．试求出点H的坐标．...更多
考考朋友
求助朋友
反馈
下一题
参考答案：
登录免费查看参考答案
参考解析：
登录免费查看参考解析
知识点：
登录免费查看知识点
答题技巧：
登录免费查看答题技巧
被用于：
暂无，欢迎编辑补充
题百科 tibaike.com 为你提供【在平面直角坐标系中， O是坐标原点，直角梯形 AO】题目的被用于哪些试卷
题目讨论 0
发布
声明：以上题目由用户自己创建，编辑，若侵犯了你的权益，请发送邮箱到feedback@deepthink.net.cn, 我们会在三个工作日内处理。
创建题目
编辑题目
题目信息：
创建者：
刷刷题用户
编辑次数：
1
难易度：
错误率：
87%
相关题目：
【简答题】（本小题满分14分） 在直角坐标系 中，以 为极点, 轴的正半轴为极轴建立极坐标系．己知圆 的圆心的 极坐标为 半径为 ,直线 的参数方程为 为参数) （Ⅰ）求圆C的极坐标方程；直线 的普通方程; （Ⅱ）若圆C和直线 相交于A，B两点，求线段AB的长.
【简答题】已知抛物线C：y2=x，F为抛物线C的焦点，O为坐标原点，则在抛物线C上且满足△OFP为等腰直角三角形的点P的个数为（ ） A．2 B．4 C．2或4 D．P点不存在
【简答题】已知：在直角坐标系中，A、B两点是抛物线y=x2-（m-3）x-m与x轴的交点（A在B的右侧），x1、x2分别是A、B两点的横坐标，且|x1-x2|=3．（1）当m＞0时，求抛物线的解析式．（2）如果（1）中所求的抛物线与y轴交于点C，问y轴上是否存在点D（不含与C重合的点），使得以D、O、A为顶点的三角形与△AOC相似？若存在，请求出D点的坐标；若不存在，请说明理由．（3）一次函数y=kx+b的...
【简答题】在平面直角坐标系内，下列各点中在第二象限的点是（ ）
【简答题】平面直角坐标系下，A点到x轴的距离为2，到y轴的距离为4，且在x轴上方和y轴的左侧，则A点的坐标是______________.
【简答题】已知抛物线y 2 =2 p x（ p >0）的焦点为F，直线L：2 p x+3y= p 2 － 。 ⑴当p为何值时，焦点F到直线L的距离最大； ⑵在第⑴题下，又若抛物线与直线L相交于A、B两点。求△ABF的面积。
【简答题】抛物线y=2x 2 -4x+9的对称轴是直线______．
【单选题】在测量平面直角坐标系中，第IV象限中的坐标增量为()
【简答题】如图，在直角坐标系中，已知点A（3，0），B（-3，0），以点A为圆心，AB为半径的圆与x轴相交于点B，C，与y轴相交于点D，E．（1）若抛物线y=13x2+bx+c经过C，D两点，求抛物线的解析式，并判断点B是否在该抛物线上；（2）在（1）中的抛物线的对称轴上求一点P，使得△PBD的周长最小；（3）设Q为（1）中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点M，使得四边形BCQM是平行四边...
【单选题】在平面直角坐标系中，位于第二象限的点是( )